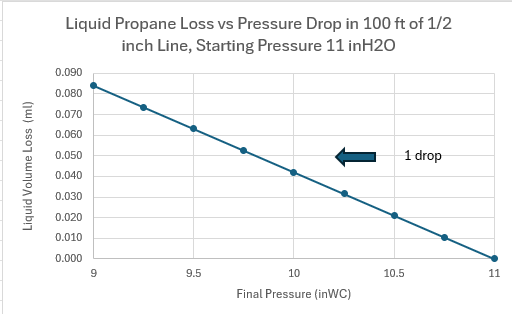
Propane is a liquid that becomes a gas (boils) at -44 deg F under atmospheric pressure. It is stored and transported under pressure in liquid form. The actual pressure of the gas above the liquid in a propane tank depends on the temperature. Tank pressure can be up to 200 psi.
Pressure regulators are used to reduce this pressure for distribution to appliances. These typically operate at 11 inches water column. That is about 0.4 psi on the above graph. Already you can see one of the more confusing aspects about propane. There are many units of measurement for both the liquid and the gas form.
Some useful conversion factors are listed below.
For liquid volume:
1 US gallon = 3.7854 liter (L)
1 cubic foot (ft3) = 28.317 liter (L) = 0.02832 cu m (m3)
1 drop = 0.00005 Liter = 0.05 milliliter (mL)
1 cubic in (in3) = 0.016387 liter (L) = 0.000016387 cu m (m3)
For gas pressure:
1 pound per square inch (psi) = 6894.8 pascal (Pa)
1 inch mercury (inHg) = 3386.4 pascal (Pa)
1 inch water (inH2O) = 249.08 pascal (Pa)
1 ounce per square inch (oz/in2) = 430.92 pascal (Pa)
The Ideal Gas Equation
There is a relationship between pressure, volume, temperature and the number of molecules in a gas.
PV = nRT
where n is the number of molecules measured in moles, P is the absolute pressure in pascals, V is the volume in cu meters and T is the temperature is degrees Kelvin. Then R is a constant equal to 8.317 Joules per mole-deg K. This equation says that equal volumes of different gases, at the same pressure and temperature, contains the same number of molecules. Knowing the atomic mass of the molecule, the total mass of the gas can then be calculated. This amazing equation was worked out in 1834!
Conversion of gas consumption in cubic feet to liquid volume in liters
Gas meters typically measure the consumption in cubic feet, but propane is sold in liquid form by volume in liters. To make this conversion, both the pressure and the temperature of the gas must be known. However, the standard pressure for most domestic appliances is always around 11 inches of water column and the local temperature is usually between 50 and 80 degrees F. The gas equation requires the absolute or total pressure which is the sum of the gauge pressure and the atmospheric pressure.
P (Pa) = 249.08 x Pgauge (inH2O) + 3386.4 x Patm (inHg)
V (m3) = 0.02832 x V (ft3)
T (degK) = [T (degF) – 32]/1.8 + 273
For example, if the gauge pressure is 11 inH2O and the atmospheric pressure is 30 inHg, P is 104,332 Pa. The volume of 1 cubic foot is 0.02832 m3, and if the temperature is 60 deg F, T is 288.6 deg K.
Putting this into the gas equation, we can calculate the number of moles in 1 cu ft of gas. It is n = 1.23 moles. The molar mass of propane is 44.1 grams per mole so multiplying this times n gives the mass of propane in 1 cu ft. It is 54.2 grams or 0.120 lbs. Finally we divide by the density of liquid propane which is 493 grams per liter to get the volume of liquid propane which is 0.110 liters. Liquid propane has an energy content of about 24,000 BTUs per liter, so the energy in 0.110 liters is 2640 BTUs.
The table below shows the ratio of liquid volume in liters to gas volume in ft3 for different temperatures and atmospheric pressures. In all cases, the gauge pressure is 11 inH2O.
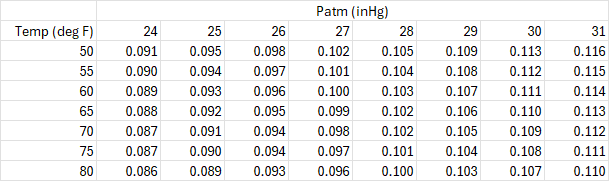
The average ratio is 0.101, but it can be 15% higher or lower depending on the temperature and atmospheric pressure.
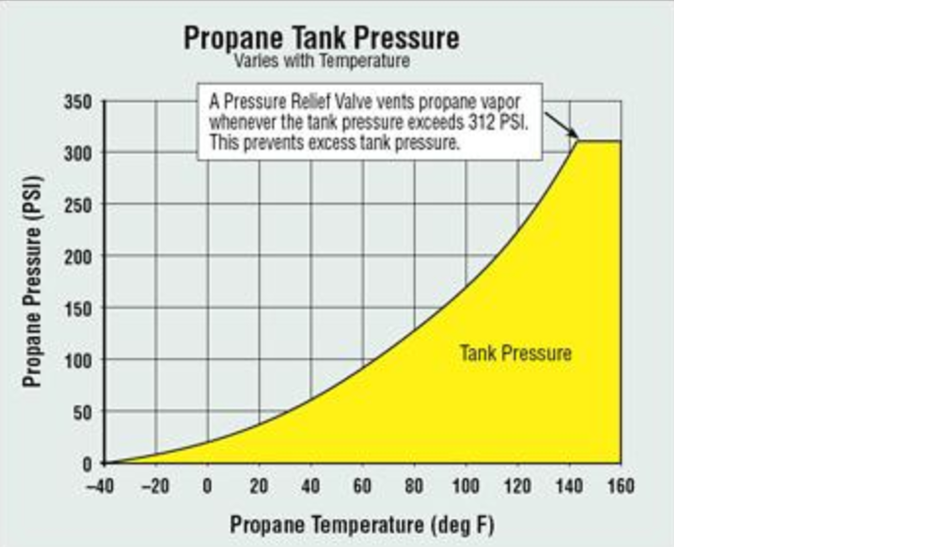
Liquid Propane Corresponding to a Pressure Drop (Leak) in a Closed Line
One of the methods for checking for a leak is to close the valve supplying pressure to the line at the regulator, then monitor the pressure in the line (with all appliances off). There is a standard test method for this which says that the pressure should remain constant over a time period of at least 3 minutes. This is very vague, however, because the resolution of the gauge used is not specified, nor is the maximum time period.
To calculate the liquid loss in a line, we need the volume of the line, the beginning and ending pressure as well as the temperature, atmospheric pressure, etc.
As an example which happens to correspond closely with the two separate low pressure lines in our house, the volume is calculated from the inside diameter (0.545 inches) and length (100 ft) of piping. This works out to 0.00458 m3. The measured temperature of 70 deg F is 294.1 deg K, and the pressure for 11 inH2O gas with 30 inHg atmospheric is 104,332 Pa. Using the gas equation, multiplying by the molar mass and dividing by the liquid density, we get 17.597 mL. If the line pressure then drops to 10 inH2O, the same calculation results in 17.555 mL, a difference of 0.042 ml. This is the amount of liquid that is lost due to the leak which showed up as a pressure drop from 11 to 10 inH2O.
It turns out that the leakage calculation is completely independent of the atmospheric pressure and nearly independent of the temperature (assuming the temperature remains constant during the test). More importantly, the amount of leakage that corresponds to a pressure drop of 1 inH2O is very small – .050 milliliter or 1 drop. The figure below shows the liquid loss vs the pressure drop.